Pointwise mutual information
Pointwise mutual information (PMI), or point mutual information, is a measure of association used in information theory and statistics.
Contents |
Definition
The PMI of a pair of outcomes x and y belonging to discrete random variables X and Y quantifies the discrepancy between the probability of their coincidence given their joint distribution and the probability of their coincidence given only their individual distributions, assuming independence. Mathematically:
The mutual information (MI) of the random variables X and Y is the expected value of the PMI over all possible outcomes.
The measure is symmetric ( ). It can take positive or negative values, but is zero if X and Y are independent. PMI maximizes when X and Y are perfectly associated, yielding the following bounds:
). It can take positive or negative values, but is zero if X and Y are independent. PMI maximizes when X and Y are perfectly associated, yielding the following bounds:
Finally, 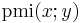 will increase if
will increase if 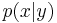 is fixed but
is fixed but 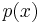 decreases.
decreases.
Here is an example to illustrate:
| x | y | p(x, y) |
|---|---|---|
| 0 | 0 | 0.1 |
| 0 | 1 | 0.7 |
| 1 | 0 | 0.15 |
| 1 | 1 | 0.05 |
Using this table we can marginalize to get the following additional table for the individual distributions:
| p(x) | p(y) | |
|---|---|---|
| 0 | .8 | 0.25 |
| 1 | .2 | 0.75 |
With this example, we can compute four values for 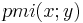 . Using base-2 logarithms:
. Using base-2 logarithms:
| pmi(x=0;y=0) | −1 |
| pmi(x=0;y=1) | 0.222392421 |
| pmi(x=1;y=0) | 1.584962501 |
| pmi(x=1;y=1) | −1.584962501 |
(For reference 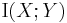 would then be 0.214170945)
would then be 0.214170945)
Similarities to Mutual Information
Pointwise Mutual Information has many of the same relationships as the mutual information. In particular,
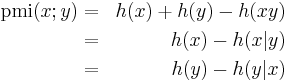
Where 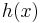 is the self-information, or
is the self-information, or 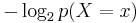 .
.
Normalized Pointwise mutual information (npmi)
Pointwise mutual information can be normalized between [-1,+1] resulting in -1 (in the limit) for never occurring together, 0 for independence, and +1 for complete co-occurrence.
![\operatorname{npmi}(x;y) = \frac{\operatorname{pmi}(x;y)}{-\log \left[ \max ( p(x), p(y) ) \right] }](/2012-wikipedia_en_all_nopic_01_2012/I/37141c23e2b1974ce5a53800bf657ac6.png)
Chain-rule for pmi
Pointwise mutual information follows the chain-rule, that is,
This is easily proven by:
External links
- Demo at Rensselaer MSR Server (PMI values normalized to be between 0 and 1)
References
- Normalized (Pointwise) Mutual Information in Collocation Extraction http://www.ling.uni-potsdam.de/~gerlof/docs/npmi-pfd.pdf
- Fano, R M (1961), Transmission of Information: A Statistical Theory of Communications, MIT Press, Cambridge, MA (Chapter 2).
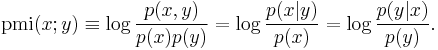
![-\infty \leq \operatorname{pmi}(x;y) \leq \min\left[ -\log p(x), -\log p(y) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/b7f13615508a5814a7ed2e46c9d26140.png)
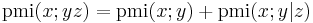
![\begin{align}
\operatorname{pmi}(x;y) %2B \operatorname{pmi}(x;y|z) & {} = \log\frac{p(x,y)}{p(x)p(y)} %2B \log\frac{p(x,z|y)}{p(x|y)p(z|y)} \\
& {} = \log \left[ \frac{p(x,y)}{p(x)p(y)} \frac{p(x,z|y)}{p(x|y)p(z|y)} \right] \\
& {} = \log \frac{p(x|y)p(y)p(x,z|y)}{p(x)p(y)p(x|y)p(z|y)} \\
& {} = \log \frac{p(x,yz)}{p(x)p(yz)} \\
& {} = \operatorname{pmi}(x;yz)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/83d4fc1d246d0ce1c02625d10b10720d.png)